数据结构
1. 二叉树
二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只有左子节点,有的节点只有右子节点。
二叉树每个节点的左子树和右子树也分别满足二叉树的定义。

Java中有两个方式实现二叉树:数组存储,链式存储。
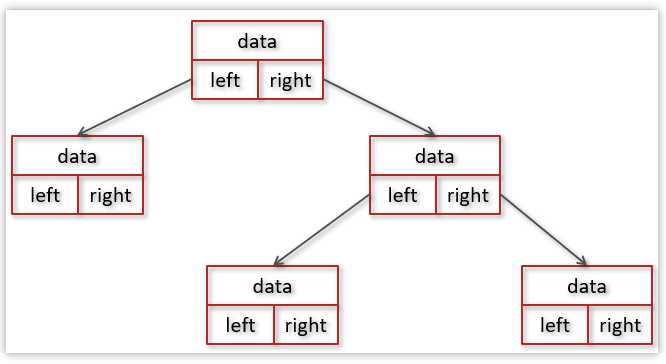
基于链式存储的树的节点可定义如下:

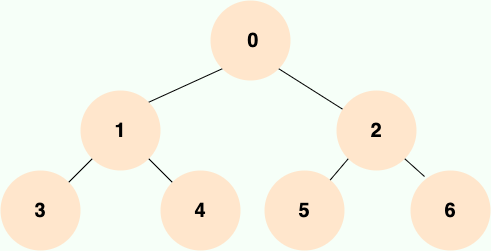
1.1 满二叉树
所有的叶子节点都在最后一层,且除了叶子节点外的所有节点都有两个子节点
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是 满二叉树。也就是说,如果一个二叉树的层数为 K,且结点总数是(2^k) -1 ,则它就是 满二叉树。如下图所示:
1.2 完全二叉树
除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点,则这个二叉树就是 完全二叉树 。
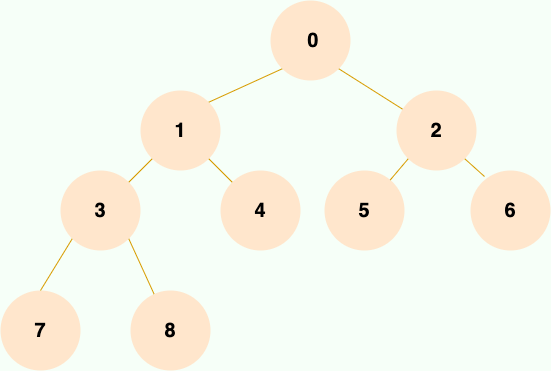
完全二叉树有一个很好的性质:父结点和子节点的序号有着对应关系。
若父结点的序号是 i,那么左子节点的序号就是 2i,右子节点的序号是 2i+1
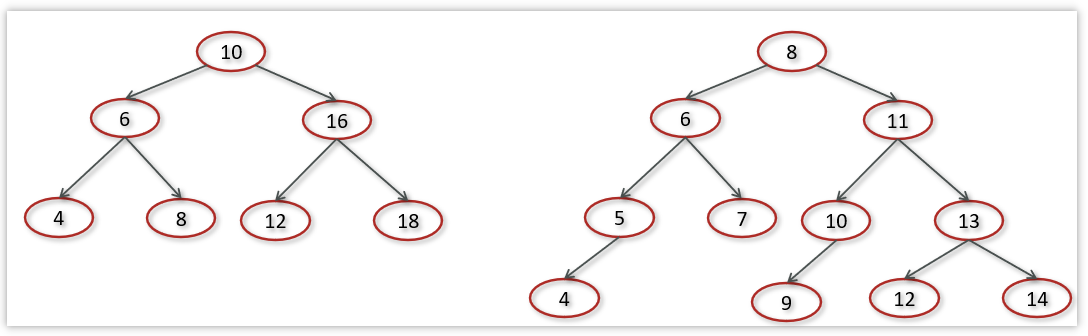
1.3 平衡二叉树(二叉搜索树)(重点)
左节点小于父节点,右节点大于父节点
时间复杂度分析
因为平衡二叉树,左边的节点永远小于父节点,右边的节点永远大于父节点,所以当你要找找一个元素时,先比较根节点。
如果目标元素比根节点还要大,那就以根节点的右节点作为父节点继续比较,无须比较根节点的左边子树。
如果目标元素比根节点还要小,那就以根节点的左子节点作为父节点继续比较,无须比较根由节点的右子树。
每次比较逗按照这个规则进行,所以每次比较都会比较都会比顺序比较少比较1/2次
所以插入,查找,删除的时间复杂度时间复杂度为O(logn)
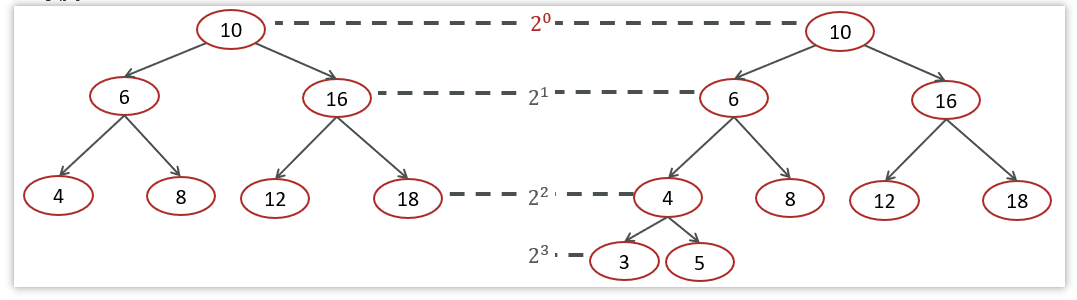
在极端情况下:
对于图中这种情况属于最坏的情况,二叉查找树已经退化成了有序的链表或者数组,左右子树极度不平衡,此时查找的时间复杂度肯定是O(n)。
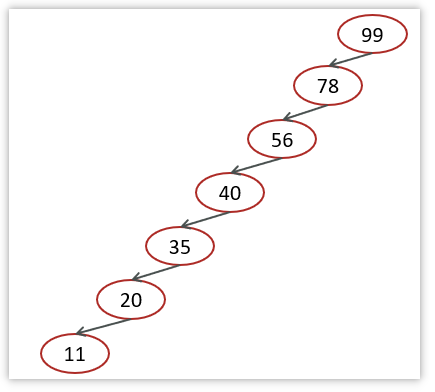
1.4 红黑树
红黑树(Red Black Tree)是一种自平衡二叉查找树,也叫平衡二叉B树
它的出现就是为了 解决平衡二叉树会出现极端的情况
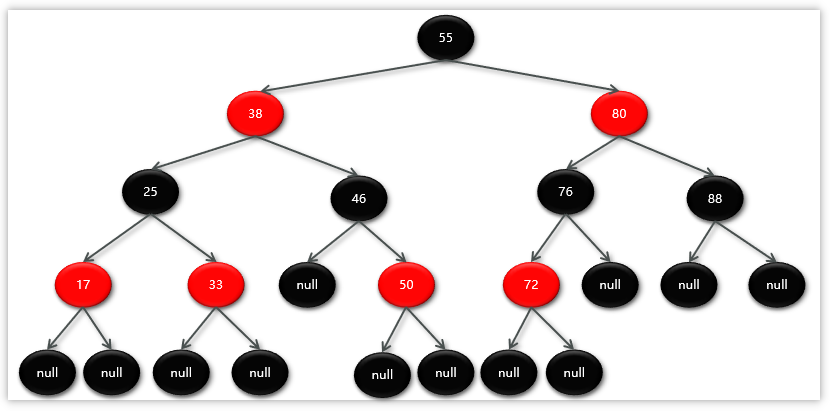
(1) 红黑树的特质
性质1:节点要么是红色,要么是黑色
性质2:根节点是黑色
性质3:叶子节点都是黑色的空节点
性质4:红黑树中红色节点的子节点都是黑色
性质5:从任一节点到叶子节点的所有路径都包含相同数目的黑色节点
比如:38 到 倒数第二层的 null,要经历两个黑色节点
38 往右走到 最后一层的 null,也是要经历两个黑色节点
38 往左走到 最后一层的null,也是要经历两个黑色节点
在添加或删除节点的时候,如果不符合这些性质会发生旋转,以达到所有的性质,保证红黑树的平衡
(2)红黑树的复杂度
查找:
红黑树也是一棵BST(二叉搜索树)树,查找操作的时间复杂度为:O(log n)
添加:
添加先要从根节点开始找到元素添加的位置,时间复杂度O(log n)
添加完成后涉及到复杂度为O(1)的旋转调整操作
故整体复杂度为:O(log n)
删除:
首先从根节点开始找到被删除元素的位置,时间复杂度O(log n)
删除完成后涉及到复杂度为O(1)的旋转调整操作
故整体复杂度为:O(log n)
